Syfte
Detta experiment gick ut på att finna samband mellan s-t- och v-t-diagram vid en accelererad rörelse samt allmänna samband mellan s-t- och v-t-diagram.
Material
Material som användes var:
- Bana med stopp
- Interface
- Vagn
- Rörelsesensor
- Datorprogrammet "PASCO Capstone"
Metod
Experimentet utfördes likadant som föregående experiment, förutom att även vagnens medelhastighet mättes och sammanställdes i en graf och tabell med hjälp av datorprogrammet.
Resultat
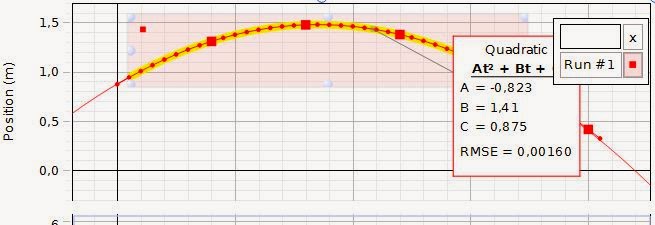
Vagnens bana i ett s-t-diagram blev:
s=-0,823t^2+1,41t+0,875
Där s=läget i meter och t=tiden i sekunder.
Här har punkter innan, precis vid och efter vagnens vändpunkt mätts ut i de båda graferna. Tabellen under visar punkterna där punkt 1 är punkten längst till vänster i diagrammen.
|
|
Tid (s)
|
Läge (m)
|
Medelhastighet (m/s)
|
Punkt 1 (innan vertex)
|
0,300
|
1,220
|
0,920
|
Punkt 2 (vid vertex)
|
0,850
|
1,480
|
2,04*10^(-4)
|
Punkt 3 (innan vertex)
|
1,50
|
1,140
|
-1,05
|
Dessa punkters medelhastighet visar vagnens momentanhastighet när den befinner sig i 3 olika tidpunkter. Vid punkt 1 (1,220m) är momentanhastigheten 0,920m/s. Vagnen rör sig alltså i positiv riktning med farten 0,920m/s. Vid punkt 2 (1,480m) är momentanhastigheten nästan 0, vilket innebär att vagnen nästan står stilla i detta tillfälle. Vid punkt 3 (1,140m), efter vertex i grafen, är momentanhastigheten -1,05 m/s. Detta innebär att vagnen åker i negativ riktning, alltså tillbaka mot rörelsesensorn, med farten 1,05 m/s.
Dessa punkters värden visar alltså vilket läge och vilken hastighet vagnen har vid en specifik tidpunkt.
Här har arean under grafen mellan två tidpunkter innan vagnens vändpunkt mätts ut, vilken är 0,46 m/s*s. Enheten här är alltså m/s*s. Om man då gör om det ena s'et till bråkform får man:
Arean under grafen visar alltså vagnens förflyttning mellan 2 tidpunkter. I detta fall är förflyttningen alltså 0,46m. Detta säger däremot inget om hur vagnen åker, utan bara att sträckan är 0,46m om vagnen åker helt rakt utan att t.ex. svänga eller dylikt. Man får däremot reda på att den kortaste sträckan som vagnen kan åka för att ta sig mellan dessa två punkter är just 0,46m, men huruvida sträckan som vagnen färdas är längre eller inte får man inte reda på.
Här har istället arean under grafen mellan två tidpunkter efter vagnens vändpunkt räknats ut. Eftersom (m/s*s) kan bytas ut mot (m) är arean under grafen alltså -0,44m. Förflyttningen mellan dessa två tidpunkter är negativ eftersom vagnens hastighet är negativ, medan tiden är positiv (vilket den i princip alltid är, då det är omöjligt att mäta tiden som negativ) och eftersom - * + = - blir då förflyttningen negativ. Detta innebär att vagnen åker bakåt, alltså tillbaka mot rörelsesensorn, vilket man även ser att den gör om man tittar på förflyttningen mellan dessa två punkter i s-t-diagrammet högst upp.
Slutsats
Sambanden man kan se mellan dessa två diagram är att i ett v-t-diagram kan man läsa ut förflyttningen (det värde som varken står på x- eller y-axeln) genom att beräkna arean under grafen mellan de 2 tidpunkter man vill veta förflyttningen. Om det istället är ett s-t-diagram man har så kan man räkna ut momentanhastigheten (som nu den varken står på x- eller y-axeln) för, i detta fall, vagnen genom att dra en tangent till grafen vars lutning man sedan kan räkna ut.